第二章 有限差分法理论基础

有限差分方法是计算流体力学中应用最多的离散化数值方法；

作为计算技术它是历史最悠久，理论上相对成熟的数值方法。

$ 2.1有限差分离散化方法

l         一个定解的流体动力学问题的数学描述；

  解法:

⑴理论（解析）解

⑵差分数值解；方程的离散，求解域（时+空）的离散，代数方程的求解，

求解域的离散化——差分分割。

l         分割尺寸（空间网格步长，时间步长）

l         （网格）结（节）点，（网格）单元

l         （边界外）虚网格点——网格沿拓。

微商（偏导数）的差商近似

1）。差商近似；一阶，二阶导数的偏心差，中心差格式

l         一阶微商的定义；       

若取消取极限过程，用，代替就是一种差商近似。称为差分格式，

      2）。差分格式的导出方法

a). Taylor’s公式；

      T.E=Truncation Error

  采用差分格式中的记法；   

          其中   

由于T.E.是 为一阶小量，故上述差商近似（差分格式）称为一阶（精度）格式

类似地可得；    (后差)

（中心差）

；（二阶导数中心差；等网格步长）

3．差分算子

l           定义以下差分算子；

  移位算子：     （当移位为+1时可省略）

算术平均算子：   

前差算子；      

后差算子；     

一倍步长中心算子：     

两倍变长中心差算子；    

讨论：

l         定义的上述差分算子，可建立彼此间的转换关系，例；

l         所有的差分算子均可用Taylor展开来估算截断误差项(余项)的量阶

例;   

*微分算子与差分算子的联系

   记微分算子:             

由Taylor公式:

 或以作为步长   

 由此，再根据差分算子之间的转换关系，可以建立微分算子与其他差分算子的联系

例1；

例2；紧致格式的引入

由微分算子与差分算子的关系有； 

  另一方面；   

由于算子最多都是只用到三个节点上的函数值，所以是仅用三点构造出了4阶精度格式，而一般地三节点格式的精度只有二阶。故称紧致格式

作业 例3；类似由可导出二阶偏导数的紧致格式为；

 例4；紧致格式应用；

令

 实际计算中分两步

上述例4实际上已经涉及微分方程的差分离散化了；或者说是直接采用差商逼近代入相应的微分方程后直接得到离散化后的微分方程。

三，偏微分方程的差分离散化――――差分方程

1.直接用差商逼近代入;

微分方程中的所有各阶偏导数分别选择适当的差商逼近,并考虑逼近的截断误差精度,从而将微分方程改写为代数的差分方程;同时得到整个差分方程对微分方程的逼近的精度.

2.由微分方程出发直接建立差分方程的几个方法,

  待定系学数离散化方法;

对于,若设是采用三节点格式,即采用

而L(u)(二阶偏导数以下)采用三节点格式,即采用  

即令;

为了确定 ，可用Tayloy展开,并与对比,使相应的偏导数项的系数相等;若为二阶算子,则偏导数有0阶,一阶和二阶三项,可建立三个方程式,正好确定  三个系数，而三阶以上的偏导数项则归到误差项中；而如果有三阶（或更高阶的）导数，则三节点格式不够，应增加节点数，才能将待定系数确定。

多项式拟合法

例方程

该方程具为特征性质，特征线为、在计算求解域中、

             斜率为

D

                                      D点值   按特征关系应与P点的值相等

C

B

A

P

n+1

n

                                                （PD为特征线，斜率为）

j-1

j+1

jJ

                                      但在差分计算中，求解域的离散形成的网格点                 

                                      是A、B、C等·P点可能并不是网格点）

                        点的值，也就是P点的值必须由A、B、C等各点的值来获得。

i)采用A.B两点线性拟合,得到P点（即D点的值）线性插值的值;

记       上式为：

               或        (FTBS格式)，当时迎.风

仍然采用线性拟合,但采用A.C两点进行插值

             整理;

               或       

                                       —Lax格式

.线性拟合，采用B.C两点外插: (思考)

抛物线拟合，用A.B.C.三点的值进行二次曲线拟合：

设：过 A、B、C三点的值，为二次抛物线 A、B、C三点的x坐标可以简单地给为，

   有             

整理得；

  ——Lax-Wendroff格式

其出发方程可认为：

分裂差分算子的离散化方法

l         若微分方程中的微分算子可作 “和”分裂,

        即

   则微分方程的差分方程可由

依序离散构成.即分裂式(2)应由(1)式得到的差分解”续接”计算 (反之亦可)

例:          

“和“式分裂为

可按下列格式计算（例取FTCS格式）

     step  1:

     step  2;

            其中：

 这种处理的理论依据是：由以上两步,可消去中间步结果

         即

最后一项容易验证

     对于时间前差格式：   上述格式与源方程的误差项同阶，可并入T.E. 考虑,而不影响差分的最后精度。证毕。

积分控制元中的离散化方法

对于守恒型(散度型)方程,除了可以在网格点上考虑网格点函数值之间的差商关系（代替微分）,从而建立差分方程外;还可以在积分控制体的有限体积内建立相应的离散积分关系,从而得到积分型的离散方程.

例,对于守恒型方程

令

由此，在任何有限域内：

若求解域离散为；

上式中最后一项是四个侧面的相关积分，四个侧面上的积分值可以分别计算。侧面面积与网格步长相关（，而每一个侧面上的值（在有限体积方法中，变量的值一般定义在体积单元的几何中心，而不在单元的侧面上）可以考虑各种不同的逼近方式，从而形成不同的格式，（类似地，的取值也可以考虑不同的逼近方式）

四).边界条件（定解条件）的离散化处理

第一类边界条件          

第二，三类边界条件

例；

一阶精度处理  

二阶精度处理：  

       网格点  

§2.2差分格式的基本性质，基本定理

一，差分格式的相容性（consistency）

  相容性表述的是：差分问题的提法与定解的微分问题在提法上的近似与否。即差分方程以及相应的定解条件的数值处理与微分方程及其定解条件是否逼近的问题。.

定义;  若微分源方程与相应的差分方程之间的截断误差项为,

     当  时,则称差分方程与微分源方程相容.

若 仅在在满足某种条件下趋于零时才成立,则称为条件相容.

二.差分格式的稳定性(stability)

1,差分计算的稳定性概念

初值问题的稳定性,(椭圆问题迭代计算的稳定性问题也可以此类比)

对同一个微分物理问题可以形成各种不同的差分计算格式;

差分计算格式包含；差分方程、初边值条件的数值处理、（离散处理）网格划分的形成，所有这些因素的综合形成一个差分计算格式，对应这一格式的解称之差分数值解；

差分计算格式对有界的初值条件，其数值解可能仍保持有界的；但也可能是无界的；有界的数值解是稳定的，无界则是不稳定的；

误差传播方程―――这一问题也可以解释为：某些格式对误差的传播是有界的，而另一些对误差的传播是无界的。

例:

      采用FTCS格式 ,当   时，其计算结果截然不同。

三，差分格式的收敛性（Convergence）

有限差分的数值解在网格步长趋于零时,数值解是否收敛于微分方程的真解。

定义：源方程的解为,其相容差分格式的离散近似解为 若：时，使 并有：

                                                       则该差分格式具有收敛性。

 在实际计算中当足够小时，若

则称之为离散化误差，分别称为（空间或时间座标的）收敛率

四，Lax等阶性定理(Lax’s Equivalence Theorem)

  对于一个适定的线性偏微分方程的初值问题,其相容的差分格式的收敛性的充分必要条件是差分格式的稳定性。       

稳定性

五,双曲型方程的CFL条件 Courant –Friedrichs –Lewy

定理: 对于双曲型方程建立的差分格式,其收敛的必要条件是差分格式的依赖域包含了相应的微分方程的依赖域

l         依赖域

六，差分格式的修正方程式 

概念：

一个物理过程的严格描述是由微分方程（组）来实现的；

差分数值解的出发方程是一个代数方程组；

差分（代数）方程（严格地说）描述了什么样的一个物理问题呢？（即使这个物理问题实际上可能并不存在！）

将这样一个设想中的物理问题，进行解析延拓后，如果改是用微分方程（组）来描述的话，那么这一个微分方程是什么样子呢？－修正方程（Modified Equations）

  意义：严格的含义下，差分方程和修正方程描述的是同一个物理问题（尽管该物理问题只是虚拟的），因此通过对修正方程各种性质的讨论将得到差分方程的基本性质；

  例：

    ——微分方程 （一维波传播方程）

差分格式（FTCB）:

上式也可以认为就是修正方程式。

但是由于上式包含对时间的任意阶偏导数，其微分方程的各种性质不易讨论，从数学上希望将上式改造成除了包含源方程的原有的各项外，只留有对空间坐标的各阶偏导数项。

即：源方程为：

将差分方程的修正方程写：成     其中R只包含u对空间坐标的各阶偏导数项。例如一维波传播方程的各种差分格式其共同的修正方程具有如下形式：

具体的数学方法是用自循环消元法，

上式重新写成：

利用列表法来实现自循环消去过程；

                                ……

（*）式      1    a       0       0        0      ……                0      0         0    …….

                       0        0      0                                       0       0

(*)                           0

(*)                               

           l    a     0   0      0     0     0  

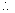修正方程式(标准形式);

  作业；（1） ；  FTCS格式的修正方程式。（保留2项）

 （2）   格式的修正方程式.

l         修正方程式的应用;

  ◆可用于分析稳定性  (详见后面对格式耗散性质的讨论)

  ◆创立新格式 (提高精度, 改善性能等)

例1：抛物方程

格式

上式格式的修正方程式是                 

                       讨论;由修正方程式;

     T。E。

令：

   则   

       即    其中：

   时  

若在的条件下, 将值代入的系数中，得：

令上式等于0：     

 在     时    

例2；Lax-Wendroff 格式的建立;

         FTCS格式;    

                      M．Eq. :

                       格式是不稳定。

    ？ 要使修正方程式中不出现 项，  有何办法?

设想从改型的源方程出发：

差分方程为：   

     这里源方程的前2项仍采用FTCS格式，其修正方程式仍同（）式；

而第三项采用空间二阶精度的中心差分格式离散，则该项对应的修正方程式，左边应为源方程中的项，右边是高阶截断误差项。其修正方程的一般式可写成为：

      从改型的方程（*）出发写出的 差分方程的修正方程是：

另一方面，这个差分方程也可以看成是与源方程（）相差的截断误差项为。

可以预见Lay-Wendroff格式的修正方程的截断误差项是：

  事实上Lax-Wendrvff格式

   M.Egs. 

当c<1 时  ,格式稳定

类似的例子；1975 Warming & Beam两步迎风格式

   P：        

C：

消去中间步相当于差分格式为：

此处右端项可以视为增加了   项

此项从何而来？请同学思考，并予以讨论。