第一章        绪论

§1.1 计算流体力学简介

（一）   什么是计算流体力学

1．以计算机作为模拟手段，运用一定的计算技术寻求流体力学各种复杂问题的离散化数值解。

l     数值解而不是解析解；

l     计算技术起关键作用；

l     与计算机的发展紧密相关

2．计算流体力学、理论流体力学、实验流体力学是流体力学研究工作的三种主要手段――既互相独立又相辅相成

n         理论分析具有普遍性――各种影响因素清晰可见、为实验和计算研究提供依据

n         实验研究仍是研究工作的基石，数值研究的许多方面都密切依赖于实验研究：实验提供数据；计算结果需由实验验证；观察实验现象分析实验数据以建立计算模型等等。

n         数值模拟是特殊意义下的实验，也称数值实验

（二）   计算流体力学研究工作的方向

1．  与现代计算技术的发展相关联的研究方向：（与计算物理，计算力学发展、图形学、网格技术等）

2．  与离散数学的理论研究相关连的研究方向；

离散化理论、边界条件数值处理的稳定性分析、格式的熵条件等

3．  在一些相关学科的边缘上寻求新的发展点；

4．  解决众多相关学科的的科研工作和工程实际提出的与流体力学问题有关的各类复杂的问题

机械、航天航空、气象、海洋、石油、环境（包括气动噪音控制）、建筑、

（三）   计算流体力学研究工作的优势、存在的问题和困难

1．优势：

“数值实验”比“物理实验”具有更大的自由度和灵活性，例如“自由”地选取各种参数等

“数值实验”可以进行“物理实验”不可能或很难进行的实验；例如：天体内部地温度场数值模拟，可控热核反应地数值模拟

“数值实验”的经济效益极为显著，而且将越来越显著；

2．问题与不足

  流动机理不明的问题，数值工作无法进行；

  数值工作自身仍然有许多理论问题有待解决；

  离散化不仅引起定量的误差，同时也会引起定性的误差，所以数值工作仍然离不开实验的验证；

§1.2 流体力学微分方程的数学性质

当微分方程转化为差分方程并用数值方法求解时，不同类型的微分方程，其数值处理方法各异，其中包括提法的适定性、物理解的性质、差分格式的适用性等；

在一些特殊的问题中，甚至通过差分格式的特殊技巧来改变方程的数学性质

（一）   一阶拟线性微分方程组的分类

对于一阶拟线性微分方程组的向量形式：

其中 为n 阶矩阵

若：的特征值为,则：

⑴．当n个特征值全部为复数时，称方程在  (t , x_i)平面上为纯椭圆型；

⑵．当n个特征值全部为互不相等的实数时，称方程在(t , x_i)平面上为纯双曲型；而当n个特征值全部为实数，但有部分为相等的实数时，称方程在(t , x_i)平面上为双曲型；

⑶．当n个特征值全部为零时，称方程在 (t , x_i)平面上为纯抛物型；

⑷．当n个特征值部分为复数、部分为实数时，称方程在(t , x_i)平面上为双曲椭圆型；

二阶拟线性方程组，可以通过降阶法进行类似的分析。(实例见后)

（二）   流体力学控制方程数学分类的举例：

1．  二维定常理想流体流动的Euler方程

写成向量形式：        

求矩阵C的特征值得：

如果：

2。二维非定常理想流体流动的Euler方程

求C的特征值，结论与定常相同：得到在X-Y平面的方程性质；

求D的特征值，得：

为四个实根，即方程在Y-t 平面为双曲型；所以Euler 方程可以在时间座标方向推进，而在定常问题中能否推进计算，必须根据流动是否为超音速（M与1的关系）来定。

3．定常不可压缩 Navier –Stokes方程的数学分类

降阶法：令：

以下的分析与一阶拟线性方程组的讨论相似，结论为定常N-S方程为椭圆型。

4．非定常不可压缩 Navier –Stokes方程

5．定常可压缩 Navier –Stokes方程

6．非定常可压缩 Navier –Stokes方程类

7．抛物化 N –S方程

利用边界层流动的概念，设X方向为主流方向，即考虑有：

把流动方向的二阶偏导数略去，（注意与边界层方程不同的是一阶偏导数都将保留！）

结论是定常N-S方程此时变为抛物型方程。

§1.3模型方程以及在计算流体力学中的应用

（一）。模型方程的引入

        简化对差分格式的性质的讨论及考核

        必须反映物理问题的最基本的特征，且方便于进行理论分析

例如：以流－涡函数描述二维流动问题时有方程：

又如：

模型方程可以提炼为：   一维Burger方程。

（二）。几个典型的模型方程

l         一维波传播方程：  

l         一维热传递方程： 

l         一维对流扩散方程：

l         Laplace方程：

l         Burger 方程：

l         无粘Burger方程：

其中前4个方程为线性方程，可求出解析解，后两个方程为非线性方程，也可以求出解析解。

▲     Burger方程的解析解：

    （1－3－1）   ：粘性系数，时为无粘方程。

解： 时，可令未知函数具有如下的形式：

                （1－3－2）

其中是待定的二阶可微分函数，将其代入（1－3－1）式：

代入（1－3－1），则得

不妨设为满足抛物方程得解 ，即：        （1－3－3）

则（1－3－2）给出了Burger方程的解析解的一般形式。

若的初始条件为，则由（1－3－2）给出的的对应于的初始条件是：

由（1－3－3）给出的Burger方程的通解是：

再代入（1－3－2）可得的解析解。特别指出，粘性Burger方程的解是连续的。

无粘Burger方程解的间断性：

类比于线性的波传播方程，可以设通解为：

讨论：

若  （1－3－5）

 表示在t-x座标中的某一个特定的点，其对应的u 为u_(s),使上式为0。

此时且

即，必定在点发生解的间断，间断的位置由（1－3－5）式确定

§1.4 计算流体力学的控制方程

（一）。概述

l         物理问题的解析解通常依赖于一些特殊形式的方程（如采用若干简化假设、选用高阶形式的方程，以避免方程个数过多等）；而对于计算流体力学的求解，由于数值计算的特点，不惧怕方程的复杂，因此可以基于更一般的方程形式，例如，可以由最基本的物理守恒律导出的普遍形式作为出发方程。

l         对于求解一个实际问题，往往需要在任意曲线坐标系下来描述，在数值计算中，需要贴体坐标系。因而，要求在任意的非正交曲线坐标系下来描述物理问题是极为平常的情况。（此点于理论的解析解是极为不同的）

l         对于理论分析，采用守恒或非守恒变量，守恒方程或非守恒方程，通常没有本质的差别，但在离散的数值计算中，守恒型与非守恒型将可能导致很大的差别，故方程的守恒性是计算流体中，必须特别注意的问题。

（二）。基本守恒律的数学描述

1．连续方程：

2．动量方程

      为粘性应力张量

3．能量方程：

（三）。直角坐标系下的守恒型方程

    不计质量力（或质量力有势），理想流体、

若考虑粘性，则：

任意非正交曲线坐标系下的守恒形式的方程

补充知识：

符号规定：直角坐标系：，单位向量：

          任意曲线坐标系： 或

           关系：

指标重复，规定为哑指标，进行遍历求和。哑指标一般写成一上一下，以便标识。

1.协变基向量：（Covariant base Vectors）

协变基向量表示的是沿坐标线的切线方向的单位向量。

2．.逆变基向量：（Contravariant base Vectors）

逆变基向量表示的是的等值面的法方向的单位向量。

在正交坐标系中，，但在任意的非正交坐标系中，协变基不平行于逆变基。

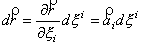
定义：

是二阶对称张量

微元弧长：

同时根据拉梅(Lame’)系数的定义:

微元面积：

微元体积：

另外，有

向量的散度：

当为常向量时，应有：

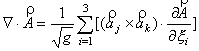
梯度：

协变基向量与逆变基向量间的关系：

将      式代入散度的表达式

张量的散度 ：

利用以上有关张量在任意曲线坐标系中的表示式，并将其代入基本守恒律方程：

l         标量方程：

    若令即为连续方程。

向量方程

令此为理想流体（无粘）条件的应力张量。

上式是向量表示式，将其写成分量式，理论上可以有许多的投影方式，实际使用中，常将任意的曲线坐标系与直角坐标系结合使用。说明如下：

在直角坐标系中，

在任意的曲线坐标系中：

                                     协变基向量

                                       逆变分量

而且：

将上式点乘：

例如：m=1 上式为：

有些文献中习惯将曲线坐标系中的逆变分量写成： ；由（  ）式:

对于粘性问题：动量方程增加了一项，

所以N-S方程：

能量方程中的粘性项部分：